Geodésicas
Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.
---------------------
Geodésica cuboctaédrica de frecuencia 3
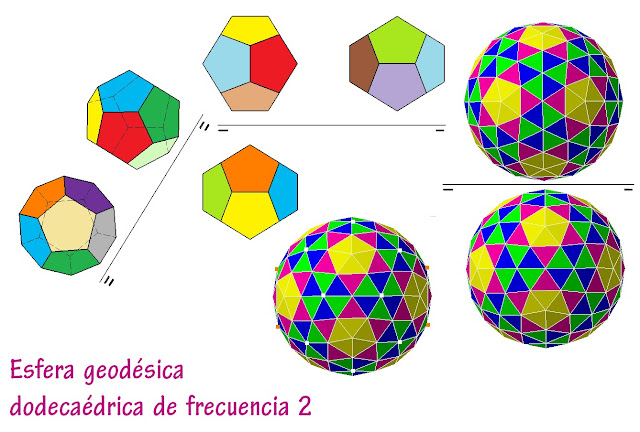
Geodésica dodecaédrica de frecuencia 1 
lunes, 8 de noviembre de 2021
En la figura 1 podemos ver dos pirámides unidas por la base, es lo que se llama una dipirámide, como las dos pirámides tienen base cuadrada, podemos girar por ejemplo la verde de manera que el centro de giro está en la base de la figura y sobre el eje e que pasa por los vértices, al hacer un giro a 45° obtenemos la configuración del número 2.
Si ahora desplazamos por ejemplo la pirámide verde en la trayectoria del eje vertical hasta que coincidan sus aristas laterales con los puntos medios de la base de la pirámide roja obtenemos la figura que aparece en el número 3.
Inmediatamente debajo tenemos la figura central pero habiendo quitado la pequeña pirámide verde superior y la pequeña pirámide roja inferior.
En el número 4 quitamos las pirámides laterales de la configuración anterior y podemos observar las dos pirámides pequeñas encima y debajo, la figura del medio es la intersección de esos dos fragmentos que quedaban debajo del número 3.
Si cogemos esa figura de intersección y le unimos las dos pirámides pequeñas de color roja y verde obtenemos en su unión la figura número cinco que es en realidad un deltoedro y cuyas proyecciones en planta y alzado aparecen en el número 6.
Podemos observar en la imagen de la izquierda las tres proyecciones en planta, alzado y perfil de un deltoedro, podemos observar que es una figura formada por deltoides, son trapecios con un eje de simetría parecidos a los rombos pero con la diferencia de que se han alargado dos lados de la figura.
En este caso tenemos que la figura tiene 8 lados, en la derecha podemos observar los cuatro deltoides para la parte superior y los otros 4 para la parte inferior, esos cuatro lados de la parte superior o inferior definen que el deltoedro sea cuadrado, por lo tanto el número de caras debe ser doble que el que refiere su designación.
En la parte central de la figura observamos el desarrollo del mismo.
Podemos observar en la Figura 1 un deltoedro de 5 caras laterales para la parte superior y otras cinco para la inferior, tenemos por tanto una figura pentagonal.
Si de la figura 2 tomamos las dos pirámides inferior y superior de manera que las bases son pentágonos regulares podemos decir que un deltoedro pentagonal está formado por un dodecaedro regular y dos pirámides simétricas respecto al plano meridiano que pasa por el centro de la figura.
En la figura 3 podemos observar el dodecaedro sin las pirámides.
En la figura 1 observamos una pirámide, si hacemos su simétrica respecto a la base obtenemos la dipirámide de la figura 5, al hacer un giro a 60º respecto al eje vertical que pasa por los vértices extremos de ambas pirámides obtenemos la configuración de la figura 2, si bajamos la pirámide roja sobre ese eje hasta que la arista lateral intercepte a la arista de la base verde obtenemos la configuración número 3, si quitamos las pirámides inferior y superior obtenemos las pirámides CD del número 4.
Si además de quitar esas pirámides quitamos también las laterales de ambas figuras, o lo que es lo mismo, si hacemos la intersección de las dos pirámides de la configuración 3 obtenemos la dipirámide u octaedro irregular del número 6, por regla general sale irregular ya que la pirámide tiene una altura cualquiera.
Si a ese octaedro irregular o o dipirámide le añadimos las dos pirámides del número 4 obtenemos el deltoedro de la figura número 7, es realmente un prisma oblicuo, y un prisma oblicuo es el caso límite de los deltoides del deltoedro que se transforman en rombos. Como podemos observar aparte de prisma oblicuo y deltoedro es también un octaedro o dipirámide oblicua a la que se le han añadido las dos pirámides del número 4.
Una vez que tomamos esta figura la representamos con sus partes constituyentes en distintos colores en el número 8 mientras que en el número 9 vemos ya las vistas en diédrico de la misma figura con las divisiones pero con los colores originales, por último al hacer la unión de la dipirámide del número 6 y las pirámides del número 4 obtenemos el prisma oblicuo de la Figura 7, 8, 9, 10.
En la Figura 11 hemos puesto el octaedro irregular apoyado en una cara, como podemos observar no es regular ya que en el perfil los vértices extremos no cortan a la arista central ortogonalmente.
En el borde superior izquierdo podemos observar un cubo cuya diagonal es el eje principal que atraviesa la figura entre vértices opuestos, alrededor de ese eje giramos un cubo de manera que dejamos registro de 5 cubos en el primer caso y de 4 cubos en el segundo, en el primer caso por ser impar observamos que los vértices de los cubos de la parte superior no coinciden sobre las verticales de los vértices de los cubos de la parte inferior, ello provoca la alternancia de aristas y que las caras laterales sean deltoides, provocando así la figura del deltoedro, como contrapartida observamos en el caso de la derecha el registro tras el giro del cubo la formación de 4 cubos y la coincidencia de los vértices superiores e inferiores provocando la coincidencia de las caras laterales en triángulos isósceles, generando de esta forma una figura formada por dos pirámides llamada dipirámide.
En este ejercicio podemos ver el caso de los 5 cubos que aparecen en el ejercicio anterior. Por la parte superior aparece en la zona izquierda la representación en sistema diédrico de la composición de los 5 cubos mientras que a su derecha aparece la intersección en deltoedro de las cinco figuras.
En la franja inferior del dibujo vemos exactamente lo mismo, el poliedro compuesto a la izquierda y la intersección a su derecha, la diferencia es que en este borde inferior la diagonal del cubo forma 45° con el plano horizontal, mientras que en el caso anterior el eje de revolución es una recta oblicua.
Podemos observar nuevamente el mismo ejercicio que en el caso anterior con la intersección de los 5 cubos, a su izquierda el poliedro resultante de la intersección y a la derecha la composición de los 5 cubos en un poliedro compuesto de figuras entrelazadas.
En el borde inferior de la imagen observamos en detalle el entrelazamiento de esos 5 cubos en su franja central, tal y como se comentaba anteriormente los vértices superiores no están alineados en verticales con los vértices inferiores provocando de esta manera una figura formada por deltoides laterales, esta figura es la que llamamos deltoedro.
Podemos observar un ejercicio afín al anterior pero ahora realizado con 7 cubos, al hacer el giro de un cubo original y tras realizar una vuelta completa observamos que se deja registro de 7 cubos y el poliedro compuesto que se forma es el que aparece en la parte izquierda de la figura, mientras que a la derecha obtenemos la intersección de esos cubos, al ser un caso impar y no haber coincidencia de vértices sobre líneas verticales sabemos que la figura resultante es un deltoedro.
Análogamente a los ejercicios anteriores, tenemos el cubo con su diagonal principal en el borde superior izquierdo, esta recta es un eje de revolución del que se dejan 7 cubos como registro en el primer caso y 2 cubos en el segundo, como podemos observar en el caso izquierdo obtenemos la figura del deltoedro mientras que a la derecha obtenemos la figura de la bipirámide, en este último caso se ha representado en el borde superior derecho la posición del eje de revolución como una línea que forma 45° con el plano horizontal mientras que en la parte inferior el eje de revolución es una recta vertical.
En el caso superior derecho de la intersección de los dos cubos observamos también la figura con el eje vertical, mientras que a su izquierda observamos el contorno en planta y alzado como un cuadrado, eso quiere decir que el eje de revolución forma en este caso los 45° con el plano horizontal.
Seguimos con el mismo procedimiento de atravesar un eje de revolución sobre figuras distintas, en este caso tenemos un cilindro elíptico que gira en torno al eje provocando el poliedro compuesto por 3 cilindros, en el borde extremo de la izquierda de la imagen observamos que el eje de revolución es una recta vertical provocando en planta una figura con tres simetrías. Como podemos observar a la derecha de ese poliedro compuesto en planta y alzado obtenemos un deltoedro como intersección de los tres cilindros.
En este caso podemos ver que los deltoides laterales del deltoedro se aproximan a rombos en el momento en que los lados de la figura coinciden en dimensión.
Volvemos a realizar un ejercicio semejante al anterior pero considerando ahora el registro de 7 cilindros y con la posición idéntica para el caso del eje de revolución respecto al cilindro elíptico.
En la parte izquierda observamos en planta y alzado en entrelazamiento de los 7 cilindros que provocan un poliedro compuesto muy complejo.
A la derecha de este poliedro compuesto observamos el deltoedro como intersección de los cilindros, esta figura representada en diédrico aparece luego dos veces representada en distintas perspectivas por la parte inferior mientras que tenemos también dos perspectivas de la composición de los cilindros por la parte inferior derecha.
Observamos un ejercicio análogo al anterior pero con 5 prismas.
En la intersección de los prismas con forma de cuña observamos una figura análoga al deltaedro pero también con trapezoides en vez de deltoides.
Podemos observar la planta y alzado de los 5 prismas y a su derecha la intersección también en sistema diédrico, así mismo podemos ver varias perspectivas del poliedro compuesto y del poliedro de intersección.
En la franja inferior podemos observar un cubo y las distintas posiciones de un eje que lo atraviesa y que es la recta que sirve para revolucionar los cubos un ángulo de 360 grados, dejando a continuación el registro de 4 figuras.
En el primer caso el eje incide en un vértice y a la mitad de la arista, en el segundo caso es la diagonal principal, en el tercer caso el eje de revolución pasa por la mitad de aristas opuestas, en el siguiente caso va desde un vértice hasta una arista opuesta, en el siguiente caso va desde un vértice hasta el centro de una cara, en el siguiente caso el eje de revolución va desde el centro de una arista al centro de una cara y por último va desde el vértice al centro de una cara.
Al girar el cubo en torno a estos ejes y generar 4 cubos se producen los poliedros compuestos que vemos por la franja central de la imagen, mientras que en la franja superior podemos observar la intersección de esos cubos.
En el primer caso a la izquierda observamos una figura formada por triángulos escalenos y deltoides, en el segundo caso por ser un número par de cubos obtenemos la dipirámide, en el tercer caso tenemos una figura formada por dos pirámides y un prisma de unión, en el siguiente caso tenemos un modelo semejante al del primer caso mientras que en el siguiente cada uno de los deltoides se fragmentan en dos triángulos, pasa lo mismo en los tres últimos casos de la derecha.
En conclusión podemos decir que el caso del deltoedro será en el segundo caso para figuras impares mientras que en los demás casos aparecen poliedros parecidos al deltoedro pero fragmentando los deltoides en 2 triángulos por regla general y salvo excepciones.
Podemos observar el caso afín al anterior pero realizado con 5 prismas hexagonales, al hacer el giro de los poliedros dejamos registro de las cinco figuras cuya composición aparece en la franja central de la imagen, mientras que a su derecha tenemos la intersección de los 5 prismas que es el deltaedro.
Por la parte inferior podemos observar varias perspectivas de las figuras.
En este caso tenemos la figura anterior también con el eje de revolución que la atraviesa de vértice a arista opuesta, en el caso número uno tenemos la planta y alzado de 5 prismas resultado de la revolución del prisma anterior, en el número dos tenemos la intersección de los prismas que nos provoca un deltoedro.
Estas figuras están en una posición oblicua, pero para hacer el dibujo más inteligible en el número 3 colocamos el eje de revolución en una posición vertical y de esta manera tenemos el poliedro compuesto en planta y alzado mientras que en el punto cuatro tenemos la intersección de esos prismas pentagonales, en el número 5 tenemos una proyección ortogonal del poliedro compuesto mientras que en el número 7 distintas perspectivas axonométricas, en el número 6 tenemos dos perspectivas axonométricas del deltoedro.
En la figura observamos nuevamente el prisma de base pentagonal regular y el eje de revolución que genera en el giro tres prismas representados en planta y alzado en el centro de la figura, a su derecha observamos otra vez el prisma oblicuo, sus caras tienen tan poca inclinación que casi parece un cubo.
Un cubo es un hexaedro regular próximo al deltoedro en el momento en que sus caras cuadradas se convierten en deltoides, en este caso las caras son romboides.
Vemos nuevamente el caso del prisma pentagonal regular y el eje de giro que deja registro de 7 prismas, en el número uno tenemos el poliedro compuesto de los 7 prismas mientras que en el número dos tenemos la intersección de los 7 prismas, es un deltoedro en la que podemos observar que sus caras laterales en deltoides.
En el número tres y cuatro tenemos distintas perspectivas axonométricas del deltoedro mientras que en el 5 y 6 tenemos los poliedros compuestos de 7 prismas.
Tenemos el prisma hexagonal regular y el eje que lo atraviesa de forma oblicua generando una composición de 3 prismas mostrados en planta y alzado en el centro de la imagen, a la derecha observamos el prisma oblicuo con sus caras que son rombos, este poliedro se llama romboedro debido a sus caras rómbicas, tenemos un caso particular en el cubo en el momento en que los rombos se transforman en cuadrados y tenemos otro caso particular en el deltaedro cuando los rombos se transforman en deltoides, como sabemos el deltoide es un trapecio con un eje de simetría.
En el número 3 y 4 vemos la perspectiva del prisma oblicuo mientras que en el 5 y 6 observamos los poliedros compuestos de 3 prismas.
En el extremo inferior de la imagen podemos ver las perspectivas de las cinco figuras antes realizadas.
Volvemos a coger el tetraedro regular que aparece en el borde superior izquierdo y hacemos el giro en torno al eje vertical provocando 7 tetraedros regulares, de esta manera obtenemos en planta y alzado el poliedro compuesto por esas figuras y cuya intersección es el deltoedro que aparece a la derecha en planta y alzado.
En la parte inferior de la imagen observamos a la izquierda el poliedro compuesto de 7 tetraedros y en la parte derecha el poliedro objeto de la intersección de los anteriores, deltoedro cuyas caras son deltoides.
En esta figura observamos en modo alámbrico por la parte inferior el caso de 5 cubos y un eje que provoca distintos poliedros compuestos al hacer el giro del primer cubo en torno al eje en distintas posiciones.
Observamos en el caso número 2 que se forma un deltoedro .
Tenemos en todos los demás casos y por regla general figuras parecidas a los deltoedros pero a veces los deltoides se fragmentan en dos triángulos o bien las figuras están compuestas por formas en deltoides conjugadas con formas en triángulos escalenos.
En el caso curioso del tercer poliedro la figura que se forma está generada por dos cucuruchos con deltoides enlazados por hexágonos regulares en su franja central.
En todos estos casos el cubo es atravesado por la diagonal principal que es considerada como eje de revolución, podemos comprobar en los casos pares que se provoca una dipirámide mientras que en los casos impares aparecen los deltoedros.
Tenemos también que en el caso 2 y 6 son coincidentes porque son múltiplos y por tanto coinciden los cubos en dos únicas figuras mientras que en el número 3 el cubo al girarlo y registrarlo tres veces provoca 3 cubos que son coincidentes consigo mismo por eso la intersección de los tres cubos es el cubo mismo de ahí que no aparezca en la figura, es un caso impar y se aproxima al deltoedro pero sus caras en vez de ser deltoides tenemos el caso límite de los deltoides que se transforman en cuadrados.
El mismo caso que los dos anteriores componiendo tanto la posición del eje vertical como la posición oblicua del eje.
A la derecha en el borde superior podemos ver la perspectiva de la dipirámide en la parte inferior el desarrollo de la misma.
3- En la figura 1 observamos una pirámide, si hacemos su simétrica respecto a la base obtenemos la dipirámide de la figura 5, al hacer un giro a 60º respecto al eje vertical que pasa por los vértices extremos de ambas pirámides obtenemos la configuración de la figura 2, si bajamos la pirámide roja sobre ese eje hasta que la arista lateral intercepte a la arista de la base verde obtenemos la configuración número 3, si quitamos las pirámides inferior y superior obtenemos las pirámides CD del número 4.
Si además de quitar esas pirámides quitamos también las laterales de ambas figuras, o lo que es lo mismo, si hacemos la intersección de las dos pirámides de la configuración 3 obtenemos la dipirámide u octaedro irregular del número 6, por regla general sale irregular ya que la pirámide tiene una altura cualquiera.
Si a ese octaedr irregular o o dipirámide le añadimos las dos pirámides del número 4 obtenemos el deltaedro de la figura número 7, es realmente un prisma oblicuo, y un prisma oblicuo es el caso límite de los deltoides del deltoedro que se transforman en rombos. Como podemos observar aparte de prisma oblicuo y deltoedro es también un octaedro o dipirámide oblicua a la que se le han añadido las dos pirámides del número 4.
Una vez que tomamos esta figura la representamos con sus partes constituyentes en distintos colores en el número 8 mientras que en el número 9 vemos ya las vistas en diédrico de la misma figura con las divisiones pero con los colores originales, por último al hacer la unión de la dipirámide del número 6 y las pirámides del número 4 obtenemos el prisma oblicuo de la Figura 7, 8, 9, 10.
En la Figura 11 hemos puesto el octaedro irregular apoyado en una cara, como podemos observar no es regular ya que en el perfil los vértices extremos no cortan a la arista central ortogonalmente.
Más a la derecha hemos colocado la misma figura y hemos hecho una copia de la dipirámide y la hemos girado 90 grados superponiendo ambas, la composición de ambas figuras genera un poliedro compuesto con el contorno de estrella de cuatro puntas que aparece en el alzado mientras que a su derecha observamos la intersección de ambos ambas dipiramides.
En el centro de la figura en color azul y verde observamos esa misma dipirámide de manera que el eje longitudinal es una recta vertical mientras que a su derecha en rojo y azul observamos nuevas proyecciones de la figura y en el borde inferior izquierdo observamos distintas perspectivas del poliedro compuesto formado por los dos cubos entrelazados.
En el centro superior de la figura observamos la posición del cubo en planta, y alzado en amarillo y azul con las proyecciones del eje de giro, según esta colocación del cubo la figura que sale al aplicar la transformación es el conjunto de cubos que aparecen a su izquierda-
En la parte inferior central de la figura aparecen los 4 cubos de manera que el eje está vertical como en la posición de su izquierda del cubo rojo, la intersección de estos cubos nos genera la dipirámide del borde inferior derecho, representada en planta, alzado y perfil.
En la parte superior derecha de la figura podemos observar con más detalle el alzado del conjunto de cubos con la intersección de las distintas caras.
Al hacer la misma transformación que en los casos anteriores, esto es, hacer un giro del cubo respecto a ese eje nos queda una composición de cubos que aparecen inmediatamente por encima de las perspectivas de esos cubos, en la parte central de la figura.
Observamos en la parte superior la intersección de esos tres cubos la obtención de distintas figuras parecidas a dipiramides. En el primer y cuarto caso las figuras están formadas por deltoides y triángulos. En el tercer caso son dos pirámides unidas por un prisma. En el quinto caso es una figura afín a la primera pero dejando los deltoides debajo y los triángulos por encima. Lo mismo en el sexto caso.
Podemos observar que en el segundo caso aparece una bipirámide. En el séptimo caso también aparece una bipirámide ya que el eje de giro coincide con el plano de la diagonal principal y su eje de giro es un segmento de vértice a vértice opuesto.
A su derecha podemos observar la intersección de ambas figuras que es realmente una dipirámide. El mismo dibujo lo podemos observar a la derecha en modo alámbrico.
En la parte inferior observamos exactamente la misma figura pero tanto la composición de los cubos como la intersección están en una posición oblicua, mientras que a su derecha observamos varias perspectivas axonométricas de la dipirámide.
En la parte inferior a la izquierda observamos otra proyección de los tetraedros con un contorno estrellado en el alzado y a su derecha una perspectiva axonométrica del octaedro regular.
A la derecha en color verde parece un octaedro regular con un eje vertical de vértice a vértice opuesto.
Al hacer un giro de esta figura en torno al eje y dejar registro de tres octaedros tras una vuelta completa obtenemos en planta, alzado y perfil la las vistas de esa figura, tal y como aparece en el borde inferior izquierdo de la imagen. Debajo del perfil aparecen los 3 tetraedros en perspectiva conformando un poliedro compuesto.
En el borde inferior observamos distintas perspectivas del poliedro compuesto y del resultado final la dipirámide de 20 caras laterales, para cada una de las pirámides.
En el borde superior izquierdo de la imagen observamos un cubo con la posición de un eje que va desde la mitad de una arista hasta el centro de la base.
La composición de todos esos cubos que aparecen por el centro son representados ahora en la franja superior, en la intersección que provoca, como podemos observar, en algún caso se da la dipirámide, como por ejemplo en el caso de 6 cubos, en el caso de 4 y 5 cubos la figura está formada por una forma semejante a una pirámide con triángulos simétricos a pares y con un deltoide que conforma la mitad de un deltoedro.
En el caso 1 aparece una dipirámide asimétrica y en el caso 2 aparece una figura parecida a un cubo con apariencia de deltoedro, ya que un cubo es realmente un deltoedro de seis caras.En las franjas inferiores podemos observar distintas perspectivas de los poliedros compuestos y de sus intersecciones.
Observamos que la planta de la figura 2 tampoco tiene todos los puntos equidistantes del centro debido a los triángulos escalenos.
En el número 4 y 5 observamos la perspectiva de la figura intersección mientras que en el 6 y 7 observamos la perspectiva axonométrica de la composición de las pirámides.
Al hacer un giro de la figura y dejar registro de cinco pirámides con ángulos iguales obtenemos en planta y alzado en el número 1 la composición de las pirámides mientras que en el número 2 obtenemos la intersección de las mismas.
En el número 4, 5, 6 y 7 observamos perspectivas del poliedro compuesto mientras que el número 9, 10 y 11 observamos la intersección de las pirámides en un nuevo poliedro compuesto por triángulos escalenos y deltoides, una figura parecida a una dipirámide.
En la parte inferior y a la derecha de la planta del poliedro intersección podemos ver varias perspectivas de ambas figuras, el poliedro compuesto y la intersección de esas pirámides.
En el número 3 y 4 observamos distintas perspectivas axonométricas de la dipirámide mientras que en el 5 y 6 observamos el poliedro compuesto formado por los 6 prismas rectos de base pentagonal regular.
Del número 3 al número 7 podemos observar distintas perspectivas axonométricas del Poliedro compuesto y de su intersección.
En la parte inferior del dibujo podemos observar distintas perspectivas de ambos poliedros compuestos y los poliedros que son objeto de la intersección de las anteriores prismas.
En el número 11 observamos los tres prismas y su posición en la dirección de los ejes cartesianos, en el número 5 observamos ya los tres prismas entrelazados generando un poliedro compuesto por los tres, en el número seis podemos observar la intersección de los 3 prismas que nos genera el rombododecaedro, también aparece la perspectiva de esta figura en el número 7, 8 y 9, en el número 12 observamos como al coger el rombododecaedro y quitarle pirámides obtenemos la figura número 10 que es una bipirámide u octaedro regular.
En el número 3 observamos los tres prismas entrelazados de manera que sus ejes coinciden con los de una axonometría isométrica mientras que en el 4 aparece la intersección de los 3 prismas, una proyección del rombododecaedro con apariencia de cubo.
Mientras en el número 9 observamos la intersección de dos tres prismas del número 2, como sabemos por el ejercicio anterior es un poliedro de Catalan llamado rombododecaedro.
En el número 11 podemos observar como al rombododecaedro le hemos cortado las pirámides de manera que obtenemos el octaedro regular del número 12, ya con el despiece de las pirámides laterales.
En el número 10 observamos la perspectiva del rombododecaedro y en el número 1 observamos los tres prismas separados con su disposición conforme a la posición de los ejes cartesianos.
Cambiamos ahora de perspectiva y observamos los mismos prismas en el lado izquierdo y los mismos números que los anteriores pero en color negro, son exactamente las mismas figuras pero bajo otra perspectiva. Es curioso en el número 9 como la proyección del rombododecaedro es una figura con apariencia de cubo en axonométrica isométrica.
Al hacer la intersección de los 4 tetraedros regulares obtenemos la dipirámide que aparece a su derecha en el centro de la figura. Más a su derecha tenemos el conjunto de los tetraedros superpuestos a la intersección de los mismos, todas las figuras superpuestas están en modo alámbrico para que se vea la coincidencia de los puntos.
En la parte inferior del dibujo podemos ver varias perspectivas del poliedro compuesto y de su intersección.
Al hacer el giro del tetraedro dejamos registro de otro tetraedro siendo el nuevo tetraedro un poliedro simétrico central respecto al centro de la figura.
En el borde superior derecho observamos los dos tetraedros entrelazados y más a su derecha la intersección de ambos tetraedros regulares, que es una dipirámide.
En el borde izquierdo de la figura podemos observar el tetraedro en color rojo y las pirámides desplegadas del despiece de manera que las cuatro figuras desencajadas del tetraedro formarían con él un cubo, tal y como vimos en la descripción del cubo de colores.
Por la parte inferior del dibujo observamos tres perspectivas del poliedro compuesto de dos tetraedros y a su derecha dos perspectivas del octaedro regular de la intersección de ambos tetraedros los anteriores, como podemos observar el octaedro regular es una dipirámide.
Al hacer un giro del cubo en una circunferencia completa y dejando registro de 2 hasta 9 cubos obtenemos los poliedros compuestos que aparecen en la parte inferior del dibujo. Como podemos observar 2 y 6 cubos provocan la misma figura ya que coinciden los ángulos, en el caso del registro de 3 cubos no aparece ya que los 120 grados que giran coinciden con sus vértices provocando una única figura y cuya intersección entre ellas es el mismo cubo, éste es un caso particular del deltoedro donde los deltoides o caras laterales se convierten en la posición límite de rombos que se transforman en cuadrados.
Observamos que en los números pares 2,4,6 y 8 las figuras que se forman son dipirámides mientras que en los impares son deltoedros, eso es debido a la coincidencia de los vértices extremos alineados en verticales en el primer caso, mientras que cuando esa coincidencia no existe y los vértices están alternos se provoca la figura del deltoedro.
Hay casos en los que el giro de los cubos coinciden con otros cubos, como en el número 9 de esta manera obtenemos menos cubos que los que se forman en el número 8 o en el número 7, pese a ser más cubos, y por tanto el poliedro resultado de la intersección de los mismos tiene menos caras.
Si ahora desplazamos por ejemplo la pirámide verde en la trayectoria del eje vertical hasta que coincidan sus aristas laterales con los puntos medios de la base de la pirámide roja obtenemos la figura que aparece en el número 3.
Inmediatamente debajo tenemos la figura central pero habiendo quitado la pequeña pirámide verde superior y la pequeña pirámide roja inferior.
En el número 4 quitamos las pirámides laterales de la configuración anterior y podemos observar las dos pirámides pequeñas encima y debajo, la figura del medio es la intersección de esos dos fragmentos que quedaban debajo del número 3.
Si cogemos esa figura de intersección y le unimos las dos pirámides pequeñas de color roja y verde obtenemos en su unión la figura número cinco que es en realidad un deltoedro y cuyas proyecciones en planta y alzado aparecen en el número 6.
El cilindro es una una superficie de revolución y reglada. Las superficies radiadas son regladas (eso quiere decir que si tomamos una generatriz de la misma podemos seguir toda su superficie con el canto de una regla) y desarrollables (se pueden extender sobre un plano) además pueden ser cilíndricas o prismáticas si el punto de contacto con la regla está en el infinito.El cilindro es también una superficie radiada que quiere decir que si tomamos una generatriz de la misma podemos seguir toda su superficie con el canto de una regla y un punto del canto de esta regla pasa siempre por un punto fijo de la superficie, esto es, que la regla toca un punto sobre la superficie de forma invariable -e ideal si está en el infinito, como el caso del cilindro o prisma.
Un prisma oblicuo a la izquierda y otro recto a la derecha. El desplazamiento o extrusión de un polígono en una trayectoria recta u oblicua genera un prisma recto u oblicuo, respectivamente. El prisma es otra superficie radiada de tipo cilíndrica porque las líneas que unen sus bases están unidas por líneas paralelas. La superficie radiada cilíndrica es un caso particular de la cónica en la que el vértice por donde pasan los radios está en el infinito. Superficie prismática es la que se genera por una recta que se mueve siempre paralela a otra y en una trayectoria poligonal quebrada que está
Un antiprisma en posición oblicua en el sistema diédrico.
Un antiprisma es aquel poliedro que tiene dos caras idénticas y paralelas de manera que una está girada respecto a otra y unidas por triángulos laterales.
Los triángulos laterales unen 2 vértices consecutivos de una base, con el vértice que corresponde a la otra.
Decimos que un antiprisma es uniforme cuando sus caras laterales son triángulos equiláteros.
En caso de que las caras no sean triángulos equiláteros lo denominamos semirregular.
Cuando las bases del antiprisma son polígonos regulares y los triángulos circundantes son equiláteros, sus aristas son todas iguales.
Parece ser que el primero que los estudió fue Johannes Kepler.
En la franja superior observamos los cinco poliedros regulares, que son aquellos cuyas caras son polígonos regulares ( con lados y ángulos iguales).
Como vemos en el dodecaedro de color magenta cortamos por dos planos paralelos que pasan por vértices de los pentágonos, inmediatamente debajo vemos la separación de las tres partes, en el centro queda el antiprisma rodeado en la parte superior e inferior por dos prismas truncados.
En el icosaedro en color marrón hacemos lo mismo, cortamos dos pirámides en cada extremo y nos quedamos con el antiprisma en la parte central tal y como se ve en el despiece inferior.
En el caso del octaedro de color verde no es necesario hacer ninguna operación ya que un triángulo y su opuesto o cara paralela están dispuestos de manera que una a girado 180° respecto a la otra, unidos los vértices de esas dos caras definen el antiprisma, realmente el octaedro regular es directamente un antiprisma.
En el caso del tetraedro rojo cortamos la figura por un corte de tipo 1, que es aquel que la corta por los puntos medios de la arista, al separar las cuatro pequeñas pirámides de los extremos nos quedamos con la figura anterior, el octaedro regular, qué es un antiprisma.
En amarillo vemos un cubo, debajo vemos el cubo cortado por dos planos y en la fila inferior observamos el cubo con el despiece en tres partes. podemos observar el antiprisma en la zona central rodeada por dos pirámides.
Observamos los cinco antiprismas en perspectiva y correspondientes al dibujo anterior, inmediatamente debajo tenemos en una posición oblicua a los antiprismas del dodecaedro y el icosaedro, así como el cubo, todos en sistema diédrico.
En la fila inferior volvemos a ver en sistema diédrico las mismas figuras en planta y alzado y apoyadas en una de sus caras poligonales. Como podemos observar el antiprisma magenta contiene un pentágono para sus bases, lo mismo el del icosaedro en color marrón, mientras que los otros tres tienen por bases triángulos equiláteros.
Una forma de construir antiprismas es a partir de un deltoedro, en el número uno vemos un deltoedro que es una figura formada por deltoides (trapezoides con un eje de simetría).
En el número 2 podemos observar esa figura ahora transformada en color verde, la hemos cortado por dos planos horizontales de manera que pasan por los puntos centrales de los deltoides.
En el número de 3 hemos separado el antiprisma, aparece como una rodaja de bases paralelas y triángulos isósceles laterales.
En el número 4 tenemos la perspectiva del deltoedro, en el 5 hemos hecho el corte y marcamos las tres piezas en 2 colores distintos, en el número 6 representamos en perspectiva axonométrica el antiprisma y en el número 7 mostramos un despiece de las tres partes que se componen del antiprisma y dos conos.
Podemos observar la construcción deltoedro a partir de la figura 1, un prisma recto que es atravesado por una diagonal denominada eje. Al hacer un giro de ese prisma respecto al eje de revolución y dejar registro en un giro de 360 grados de 5 prismas obtenemos la figura 2.
En la figura 3 tenemos la intersección de esos prismas que es un deltoedro, en el número 4 hemos cortado el deltaedro por dos planos paralelos que pasan por vértices de los deltoides, en el 5 hemos separado las tres piezas constituidas por un antiprisma y dos pirámides, en el número 6 cogemos el antiprisma y marcamos un eje de revolución en su cara superior, al hacer un giro de 360 grados de la figura sobre este eje y luego un giro de 180 grados en el plano donde se apoya obtenemos la figura número 7.
En el número 8 superponemos ambos antiprismas obteniendo lo que se llama un antiprisma estrellado, en el número 9 calculamos la intersección de ambos antiprismas obteniendo dos pirámides truncadas unidas por la base.
Mostramos nuevamente las figuras correspondientes a la transformación anterior, en el número 1 tenemos el deltoedro que de su truncamiento obtenemos el antiprisma del número 5, en el 4 hacemos los dos giros, el espacial a 360º y el plano a 180°, en el 3 superponemos ambos prismas teniendo este poliedro compuesto y estrellado y en el 2 calculamos la intersección de ambos antiprismas, obteniendo la nueva figura de dos pirámides truncadas.
En la franja inferior podemos observar las mismas figuras numeradas en azul pero ahora en sistema diédrico con sus proyecciones en planta y alzado.
No hay comentarios:
Publicar un comentario