Evolvente de una circunferencia

Construimos una circunferencia y la dividimos en partes iguales, 12 por ejemplo. En cada uno de los puntos donde los diámetros cortan a la circunferencia T1, T2, T3, T4, etc., hacemos rectas tangentes a la circunferencia: T1-A, T2-B, T3-C, etc.
Con centro en T1 y radio T1-T12 hacemos un arco hasta T1-A, punto de corte con la 1ª recta tangente A.
Con centro en T2 y radio hasta donde concluye el primer arco anterior hacemos el segundo arco hasta B.
Con centro en T3 y radio hasta donde concluye el 2º arco anterior hacemos el 3º arco hasta C y así sucesivamente.
La evolvente es el dibujo que hace un punto del extremo de un cordel que se desenrolla de una circunferencia. Un ejemplo de esta curva lo tenemos en el flanco de una rueda dentada.
La evoluta de la evolvente del círculo, esto es, el lugar geométrico de los centros de curvatura de la evolvente es la circunferencia en la que se hace centro para realizar los arcos de la espiral.

El lugar geométrico de los centros de curvatura de cualquier curva es una evoluta. Por tanto la evoluta de esta espiral evolvente de la circunferencia es una circunferencia.
Óvalos

Método general
Se trata de hacer una figura parecida a la elipse pero que se pueda trazar con arcos de circunferencia. Dados los semidiámetros mayor, AB y menor, BM. Se traza la circunferencia de radio AB y centro en B. Con centro en M se traza la circunferencia tangente a la anterior. Se une M y A, segmento que corta a la circunferencia de centro M en D.
Se hace la mediatriz h de AD y corta a AB en T y a BM en U.
T y U son los centros de las circunferencias que generan el óvalo. (Del otro lado serán los puntos simétricos de éstos respecto a los ejes).

En las tres figuras a color podemos ver resuelto el ejercicio anterior tomando diferentes tamaños en las circunferencias superiores de manera que el eje menor del óvalo tenga distintas longitudes. Observamos que cuanto mayor es esa circunferencia interior, más excéntrico o alargado es el óvalo, observamos también los puntos A B en los que se hace centro con el radio correspondiente y sus puntos simétricos, centros de los arcos simétricos respecto a los dos ejes del óvalo.

Dos circunferencias enlazadas mediante el arco CD. El punto de tangencia que enlaza el arco mayor y menor del óvalo está alineado con los dos centros de los dos arcos.

Este método se viene haciendo para construir un ovoide dado el eje menor, no obstante si hacemos la simétrica respecto a la vertical tenemos un óvalo. Se hacen los dos diámetros ortogonales de la circunferencia y en los puntos de corte con ella S M se pasa una recta. Se hace centro en S con la distancia ST hasta que corte a la prolongación de SM en el que va ser el punto de tangencia C. Se hace centro en el punto M y con el radio MC construimos el arco que nos queda.

Construcción de un óvalo dentro de un cuadrilátero en forma de rombo. Por C , vértice superior del eje menor, se hace una perpendicular a la recta DB, este es el punto de tangencia que enlaza el arco de centro C y radio CP’. El centro del otro arco O2 es la intersección de la recta CP’ con el eje AB.
 Construcción de un óvalo dado el eje mayor. Dividimos el eje mayor en tres partes iguales y hacemos dos circunferencias tomando como centro las divisiones interiores. En la intersección de las dos circunferencias hacemos centros O1 O2 para enlazar ambas con un arco mayor. Si alineamos los puntos de intersección de las circunferencias O3 O4 con los centros de las dos circunferencias O1 O2 tenemos una recta que corta a las dos circunferencias en los puntos de tangencia donde se enlaza el arco mayor con el menor.
Construcción de un óvalo dado el eje mayor. Dividimos el eje mayor en tres partes iguales y hacemos dos circunferencias tomando como centro las divisiones interiores. En la intersección de las dos circunferencias hacemos centros O1 O2 para enlazar ambas con un arco mayor. Si alineamos los puntos de intersección de las circunferencias O3 O4 con los centros de las dos circunferencias O1 O2 tenemos una recta que corta a las dos circunferencias en los puntos de tangencia donde se enlaza el arco mayor con el menor.ÓvaloThis is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com |
Espiral de Arquímedes

Hacemos circunferencias concéntricas equidistantes (en verde) y dividimos las circunferencias en un número de diámetros 1, 2, 3, 4, 5, etc., que las corten en sectores circulares iguales, por ejemplo de 30º.
La línea que va del centro N a la intersección de la primera circunferencia con el primer diámetro 1 nos genera la 1ª curva de la espiral. La 2º circunferencia con el 2º diámetro 2 nos genera la siguiente curva de la espiral, etc.
 Como toda espiral, es una curva abierta y plana y se genera por un punto que se desplaza uniformemente a lo largo de una recta que gira en torno a uno de sus extremos con una velocidad angular constante. La curva que se enrolla sobre sí misma crece uniformemente en progresión aritmética, esto quiere decir que la distancia de un brazo a otro siempre se genera sumando la misma dimensión. Un ejemplo práctico de la espiral de Arquímedes lo tenemos en la trompa de la mariposa, en los dibujos y ornamentos de la cerámica que se aplican por desplazamiento del pincel en la figura torneada, en los muelles de compresión de líquidos y gases, en muelles de relojes, en los surcos de los discos de vinilo, en los fósiles y en todas las formas espirales en las que las distancias entre los brazos son siempre constantes o en los que en cada rotación hay siempre una contracción o dilatación constante.
Como toda espiral, es una curva abierta y plana y se genera por un punto que se desplaza uniformemente a lo largo de una recta que gira en torno a uno de sus extremos con una velocidad angular constante. La curva que se enrolla sobre sí misma crece uniformemente en progresión aritmética, esto quiere decir que la distancia de un brazo a otro siempre se genera sumando la misma dimensión. Un ejemplo práctico de la espiral de Arquímedes lo tenemos en la trompa de la mariposa, en los dibujos y ornamentos de la cerámica que se aplican por desplazamiento del pincel en la figura torneada, en los muelles de compresión de líquidos y gases, en muelles de relojes, en los surcos de los discos de vinilo, en los fósiles y en todas las formas espirales en las que las distancias entre los brazos son siempre constantes o en los que en cada rotación hay siempre una contracción o dilatación constante.Cuadriláteros con vértices sobre espirales arquimedianas.
Espiral de Durero en rectángulo áureo

Hacemos un cuadrado de base CD. En su punto medio M y con radio MA (A es el vértice superior derecho del cuadrado) hacemos el arco que corta a CD en B.
Levantando por B una vertical y por A haciendo una horizontal encontramos en su intersección el punto T. El cuadrado original más el rectángulo ATDB es un rectángulo áureo y éste último es proporcional a la suma de los dos. Por analogía, dentro de ATDB podemos ubicar otro cuadrado de lado AT y así hasta el infinito.
Dentro de cada rectángulo que obtenemos por este procedimiento colocamos un cuadrado.
Para construir la espiral, hacemos centro en D (O1) con radio DC y obtenemos el primer arco. Luego, con centro en O2 y radio O2-A hacemos el 2º arco, después con centro en O3 y radio hasta donde concluye el último arco hacemos el 3º. Procedemos análogamente con los siguientes arcos, centro en O4, O5, etc.
http://la-proporcion-aurea blogspot.com/

AB=AE+EB; AB/AE=AE/EB
la espiral de Durero, mal llamada logarítmica, pero muy análoga en forma y propiedades, tiene un crecimiento de anchura uniforme y continua. Es una espiral equiangular y la distancia entre sus brazos se incrementa en progresión geométrica, esto quiere decir que en vez de ir sumando la misma dimensión para pasar de un brazo al otro como pasa con las de progresión aritmética, pues hay que multiplicar por un número constante cada brazo. Por ejemplo si un brazo pasa por el punto 1 y crece en una progresión constante de dos unidades, el siguiente tramo pasará por el punto 2, el siguiente por el 4, el siguiente por el 8, el siguiente por el 16, etc. Obtendremos los siguientes puntos multiplicando por dos.
Es una espiral que se da en los tornados, en las conchas de moluscos, en la trayectoria que siguen los insectos para buscar la luz, en la trayectoria que sigue el halcón para cazar su presa, en las galaxias, en las telas de araña, en las superficies de fallas, en las curvas de la borrasca, en la concha del caracol, en las de las piñas, en la estructura de las curvas de la superficie del erizo, en los desagües, en las curvas de dónde salen las cuerdas de los violines, en los bordes de las rosas de los pétalos, etcétera.

En un rectángulo áureo (el rojo más el azul) hacemos una circunferencia con centro en B y con el radio BC. Hacemos otra verde con centro en A y radio AB. La intersección de las 2 nos determina el punto M, que junto a A y B definen el triángulo áureo, señalado con una trama verde.

Para obtener la espiral hacemos centro en D con radio DC y hacemos un arco hasta B. Hacemos centro en M y con radio MB hasta A.
Hacemos centro en E y con radio EA hasta D.
Hacemos centro en F y con radio FD hasta M.
Hacemos centro en G y con radio GM hasta E. Etc.
Ovoide
Volutas
http://poligonos-regulares.blogspot.com.es/
| http://poligonos-regulares-dinamicos.blogspot.com.es/ |
 Aquí observamos la voluta con sus centros respectivos. Observamos que la zona comprendida entre dos radios vectores genera arcos concéntricos.
Aquí observamos la voluta con sus centros respectivos. Observamos que la zona comprendida entre dos radios vectores genera arcos concéntricos. Voluta de tres centros y un paso. Hacemos centro en el punto a con la distancia AC hasta que corte a la prolongación de la recta AB. Hacemos centro en el punto B con la distancia BJ hasta que corte a la prolongación de la recta BC en el punto K.
Voluta de tres centros y un paso. Hacemos centro en el punto a con la distancia AC hasta que corte a la prolongación de la recta AB. Hacemos centro en el punto B con la distancia BJ hasta que corte a la prolongación de la recta BC en el punto K. Espiral cuya matriz es un pentágono regular.
Espiral cuya matriz es un pentágono regular.En el momento en el que un polígono incrementa su número de lados hasta transformarse en una circunferencia, la voluta se convierte en la envolvente del círculo.
--------------------------------------------------------
Triángulo más cuadrado en la figura
Podemos ver un triángulo equilátero y un cuadrado que tienen sus lados del mismo tamaño, la voluta genera los dos primeros arcos a b idénticos en ambas figuras hasta que b toca al lado que es la prolongación del cuadrado y que genera la voluta.
Como la espiral del cuadrado se abre más que la del triángulo, llega un momento tras su separación de la espiral del triángulo, en el que vuelve a coincidir con ella, y lo hace siempre de forma cíclica y constante. Esto ocurre, según vemos en el dibujo en las franjas c y d.
En el dibujo aparece señalados los arcos coincidentes de forma cíclica.

Construimos un polígono regular y prolongamos sus lados. Hacemos centro en uno de sus vértices 1 con radio la longitud de un lado del polígono 1-3. Hacemos a continuación centro en el vértice consecutivo 2 y radio el que se determina hasta el punto donde termina el último arco de radio 1-3. Procedemos así sucesivamente con los demás puntos.
VolutaThis is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com |
Cicloides, epicicloides e hipocicloides


Para construirla dividimos la circunferencia por ejemplo, en 8 partes iguales, la rectificamos, esto es, la convertimos en una línea cuya longitud es el diámetro por pi (long. de la circunferencia = 2.PI.R).
Cogemos el diámetro de la circunferencia y lo extendemos 3,14 veces sobre la base de la misma a partir de P.
Dividimos en 8 partes iguales el segmento rectificado por la línea 6-2 a partir del centro de la circunferencia.
La intersección de la circunferencia de centro 01 y mismo radio que la original con la línea 7-1 nos genera el primer punto.
La intersección de la circunferencia de centro 02 y mismo radio que la original con la línea 6-2 nos genera el segundo punto.
La intersección de la circunferencia de centro 03 y mismo radio que la original con la línea 5-3 nos genera el tercer punto, etc.
 El área bajo la curva es tres veces la circ. que gira, esto quiere decir que las tres regiones (amarillo, verde, azul), tienen igual área.
El área bajo la curva es tres veces la circ. que gira, esto quiere decir que las tres regiones (amarillo, verde, azul), tienen igual área. El lugar geométrico de los centros de curvatura se llama evoluta, como podemos ver la evoluta de la cicloide es ella misma.
El lugar geométrico de los centros de curvatura se llama evoluta, como podemos ver la evoluta de la cicloide es ella misma.Espiral logarítmica

La espiral logarítmica es aquella que tiene sus radios crecientes en progresión geométrica y que está formada por triángulos rectángulos semejantes superpuestos, en los que la hipotenusa de cada uno es el cateto del siguiente.
Los triángulos rectángulos se apilan unos sobre otros por una rotación más dilatación en la que el vértice del primero es el centro invariante de todos los demás triángulos que se van generando.

En el dibujo podemos ver la diferencia entre una espiral arquimediana (verde) y otra logarítmica (azul). Para dibujarlas se ha hecho una radiación o conjunto de líneas que pasan por un vértice, todas con el mismo ángulo entre ellas, lo que se denomina una transformación matricial polar así como un conjunto de circunferencias concéntricas equidistantes.
La intersección de las líneas de la radiación con las circunferencias equidistantes nos determinan los puntos de las espirales. La diferencia entre las dos espirales radica en un distinto crecimiento.
La espiral arquimediana crece sumando siempre una unidad sobre el número anterior: 1, 2, 3, 4, 5, 6, 7, etc., es lo que se llama una progresión aritmética mientras que en la espiral logarítmica tenemos que multiplicar el punto anterior por uno dado para obtener el siguiente número, por ejemplo 2 × 2 igual a 4, 4 × 2 igual a 8, 8 × 2 igual a 16, etc., es lo que se llama una progresión geométrica.

El dibujo muestra el crecimiento uniforme de la espiral arquimediana en color rojo en contraste con la espiral logarítmica azul, de crecimiento en progresión geométrica.
Curvas construidas por inversión
La inversa de una espiral arquimediana es una espiral hiperbólica. La espiral hiperbólica tiene por ecuación polar:
r θ = a
Curvas y superficies. Generación y clasificación

VÍDEOS DE DIBUJO TÉCNICO Y GEOMETRÍA CLASIFICADOS POR TEMAS
Vídeos del sistema diédrico:
http://videos-de-dibujo-tecnico-y-geometria.blogspot.com.es/2014/04/sistema-diedrico.html
http://teoremas-de-geometria.blogspot.com.es/2012_03_01_archive.html
Curvas y elementos.
Un punto que se desplaza describe una curva, por lo que se puede definir ésta como el lugar geométrico de las distintas posiciones de un punto que se mueve.
Cuando el elemento que se mueve es una línea genera una superficie, por ello se puede definir como el lugar geométrico de las distintas posiciones de una línea.
Una superficie en general es también la parte límite de un cuerpo, el término de la superficie, es aquello que está en contacto con el exterior, con el espacio circundante. En la superficie sólo se pueden considerar dos dimensiones ya que no tiene volumen.
Las curvas pueden ser planas o alabeadas.
Si el punto que genera la curva se mueve en el plano genera una curva plana, si lo hace fuera del plano una curva alabeada. La curva alabeada se denomina también de doble curvatura.
Elemento rectilíneo es el segmento que une dos puntos infinitamente próximos de la curva.
Secante es el segmento que une dos puntos distantes de la curva.
Tangente es el límite de la secante de dos puntos infinitamente próximos. Es la prolongación del elemento rectilíneo.
Normal es la perpendicular a la recta tangente trazada en un punto de la curva.
Ángulo de contingencia es aquel definido por dos tangentes de la curva.
Círculo osculador es aquel que coincide con tres puntos de la curva.
Centro de curvatura es el centro del círculo osculador.
Radio de curvatura es el del círculo osculador.
Curvatura total es el ángulo de contingencia de tangentes extremas de la curva.
http://curvas-planas.blogspot.com/
http://curvas-conicas.blogspot.com/
Definición de superficie: Una superficie es el lugar geométrico de las posiciones distintas de una línea o curva en el espacio. Una superficie es la envoltura que circunda a un cuerpo. Los planos directores o directrices son los que establecen el movimiento de la generatrices de la superficie. Pueden ser limitadas o ilimitadas según que contengan un volumen finito dentro de un cuerpo o no. Superficie tangencial es aquella que tiene una línea común como otra superficie, sin cortarla ni atravesarla.
Superficie plana es aquella en la que se pueden trazar líneas rectas en cualquier dirección de la misma.
Superficie envolvente es la que genera distintas posiciones de otra superficie llamada involuta.
 La superficie es reglada por estar formada por cilindros (intersección de 3 cilindros iguales de ejes concurrentes ortogonales). Los cilindros son superficies cuyas generatrices pueden seguirse con una regla tocando todos sus puntos.
La superficie es reglada por estar formada por cilindros (intersección de 3 cilindros iguales de ejes concurrentes ortogonales). Los cilindros son superficies cuyas generatrices pueden seguirse con una regla tocando todos sus puntos.
Superficies desarrollables son las que se pueden extender sobre un plano sin deformación, como por ejemplo las superficies cilíndricas y cónicas. Dos generatrices infinitamente próximas se cortan. Si un plano es tangente a la superficie en un punto lo es en toda la generatriz que pasa por ese punto,
por regla general cualquiera de estas propiedades son suficientes para que la superficie sea considerada desarrollable.
Superficies radiadas son las que se generan por el movimiento de una recta apoyada en un punto propio o impropio y sobre una línea o curva.
Superficies alabeadas son las que no se pueden desarrollar y tienen sus generatrices infinitamente próximas. La superficie alabeada es la que siendo reglada (que quiere decir que se puede hacer con líneas rectas) no se puede desarrollar (que quiere decir que no se puede extender sobre un plano sin deformación). Un plano tangente a las mismas en un punto contiene a su generatriz pero no es tangente a la superficie en otros puntos de la generatriz.
 Superficies alabeadas son las que se generan por el movimiento de una línea recta de forma que dos posiciones adyacentes de una recta se cruzan. En la figura un conjunto de líneas rectas se apoyan en otras dos, llamadas directrices, generando una superficie reglada alabeada.
Superficies alabeadas son las que se generan por el movimiento de una línea recta de forma que dos posiciones adyacentes de una recta se cruzan. En la figura un conjunto de líneas rectas se apoyan en otras dos, llamadas directrices, generando una superficie reglada alabeada.Una curva alabeada es una línea en la que todos sus puntos no están sobre el plano.
Superficie alabeada y superficie reglada alabeada son sinónimos, se utilizan indistintamente.


Clasificación de las superficies alabeadas: las generatrices deben apoyarse siempre sobre tres directrices:
1- Se apoya sobre tres directrices sin perder en ningún momento el contacto con ellas.
En este caso tenemos el hiperboloide elíptico y de revolución, construidos sobre tres líneas rectas.
Curvas alabeadas construidas con dos líneas rectas y una curva.

 Curvas alabeadas construidas con una línea recta y dos curvas, por ejemplo el cuerno de vaca o paso oblicuo.
Curvas alabeadas construidas con una línea recta y dos curvas, por ejemplo el cuerno de vaca o paso oblicuo.2- Se apoyan en dos líneas directrices y siempre están paralelas a un plano director.
Apoyado sobre dos líneas rectas tenemos el paraboloide hiperbólico.
Apoyado en una línea recta y una curva tenemos el conoide y el helicoide recto.
Apoyado en dos líneas curvas tenemos el cilindroide.
3- Se apoyan en dos líneas directrices y forma la generatriz siempre un mismo ángulo con algún plano.
Apoyado en dos líneas rectas tenemos el hiperboloide concoideo
Apoyado en una línea recta y una curva tenemos el helicoide oblicuo.
Apoyado en dos líneas curvas tenemos el helicoide oblicuo.
Todas las superficies alabeadas son siempre regladas, esto quiere decir que se pueden generar con una línea recta. Si en un punto de una superficie reglada sólo se puede trazar una línea recta y no más se dice que la superficie reglada es simple, también denominada reglada simple o de simple reglaje. Si se pueden trazar dos será de doble reglaje. Las superficies de doble reglaje son el hiperboloide elíptico y el paraboloide hiperbólico.
 El paraboloide hiperbólico está generado por una recta que se apoya en dos líneas directrices y siempre se mantiene paralela a un plano llamado director. Existe otro conjunto de generatrices consideradas como directrices y un plano paralelo a estas directrices definido como nuevo plano director.
El paraboloide hiperbólico está generado por una recta que se apoya en dos líneas directrices y siempre se mantiene paralela a un plano llamado director. Existe otro conjunto de generatrices consideradas como directrices y un plano paralelo a estas directrices definido como nuevo plano director.Paraboloide hiperbólico en perspectiva caballera
El conoide es una superficie reglada alabeada con un plano director y dos directrices, una rectilínea y otra curva. Si la directriz curva es un círculo se tiene el conoide circular, si es una elipse tenemos el conoide elíptico, etc.
 Si consideramos dos rectas que se cruzan y una de ellas es el eje de revolución al girarlas, se engendra un hiperboloide de una hoja.
Si consideramos dos rectas que se cruzan y una de ellas es el eje de revolución al girarlas, se engendra un hiperboloide de una hoja.
Secciones cónicas del hiperboloide.
Dibujar un hiperboloide de una hoja con triángulos equiláteros
Trazas de un hiperboloide de una hoja
Hiperboloide de 1 hoja en perspectiva caballera y diédrico
Hiperboloide de 1 hoja (el reglado alabeado) en axonometría isométrica
Hiperboloide circular y elíptico de una hoja
Ángulo de inclinación de generatrices de hiperboloide de una hoja
 El paraboloide hiperbólico es una superficie reglada alabeada, se puede construir con líneas rectas y al mismo tiempo es de doble curvatura. Dos rectas muy próximas del paraboloide hiperbólico se cruzan y es una superficie que no se puede desarrollar. El paraboloide hiperbólico está construido por líneas rectas que se apoyan en parábolas, estas son las curvas directrices de la superficie.
El paraboloide hiperbólico es una superficie reglada alabeada, se puede construir con líneas rectas y al mismo tiempo es de doble curvatura. Dos rectas muy próximas del paraboloide hiperbólico se cruzan y es una superficie que no se puede desarrollar. El paraboloide hiperbólico está construido por líneas rectas que se apoyan en parábolas, estas son las curvas directrices de la superficie.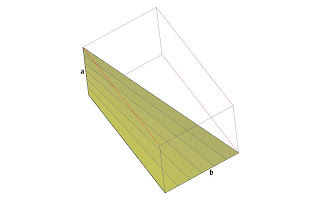 Otro paraboloide hiperbólico pero con menos curvatura, se forma por rectas (generatrices) apoyadas en dos rectas que se cruzan a b (directrices). Los planos paralelos que contienen esas rectas determinan uno de los planos directores, el otro es perpendicular a ambos. Un plano director de una superficie es el plano que se puede mantener siempre paralelo a una generatriz de la misma. De los dos planos directores se desprende que la superficie tiene generatrices de dos sistemas distintos que se cortan, mientras que las del mismo sistema paralelas a un plano director se cruzan.
Otro paraboloide hiperbólico pero con menos curvatura, se forma por rectas (generatrices) apoyadas en dos rectas que se cruzan a b (directrices). Los planos paralelos que contienen esas rectas determinan uno de los planos directores, el otro es perpendicular a ambos. Un plano director de una superficie es el plano que se puede mantener siempre paralelo a una generatriz de la misma. De los dos planos directores se desprende que la superficie tiene generatrices de dos sistemas distintos que se cortan, mientras que las del mismo sistema paralelas a un plano director se cruzan. En la figura de la izquierda podemos observar en la parte superior con el número uno un paraboloide hiperbólico inscrito en un cubo, podemos ver que las generatrices se apoyan siempre en un conjunto de 4 parábolas, todas las generatrices -que se han puesto en cuatro colores- son siempre paralelas a un plano diagonal que pasa por dos aristas opuestas del cubo. En la figura número dos podemos ver otro tipo de unión, vemos que el tramo que está más a la derecha se une mediante generatrices con un tramo parabólico más cercano y en consecuencia la figura no es un paraboloide hiperbólico.
En la figura de la izquierda podemos observar en la parte superior con el número uno un paraboloide hiperbólico inscrito en un cubo, podemos ver que las generatrices se apoyan siempre en un conjunto de 4 parábolas, todas las generatrices -que se han puesto en cuatro colores- son siempre paralelas a un plano diagonal que pasa por dos aristas opuestas del cubo. En la figura número dos podemos ver otro tipo de unión, vemos que el tramo que está más a la derecha se une mediante generatrices con un tramo parabólico más cercano y en consecuencia la figura no es un paraboloide hiperbólico. Dos secciones distintas de una figura con caras en paraboloides hiperbólicos. Si el plano de corte coincide en su desplazamiento con un plano director tenemos como sección un polígono, si el corte es oblicuo tenemos por lo general una figura formada por hipérbolas.
Dos secciones distintas de una figura con caras en paraboloides hiperbólicos. Si el plano de corte coincide en su desplazamiento con un plano director tenemos como sección un polígono, si el corte es oblicuo tenemos por lo general una figura formada por hipérbolas.Superficie compuesta es aquella engendrada o constituida por la combinación de otras.
Tangentes a una superficie.
La recta tangente a una superficie en un punto es la tangente en ese punto a cualquier curva de la superficie.
El plano tangente a la superficie en un punto es el lugar geométrico de todas las tangentes que pasan por ese punto.
Un plano es normal a una superficie en un punto cuando lo es al plano tangente a la superficie en el mismo punto.
Superficies curvas son las que se engendran por el movimiento de una curva pero que no se pueden desarrollar ni alabear.
Axonometría isométrica de 7/8 de volumen de revolución de 2 toros y escocia
Superficies de revolución de doble curvatura: un cono es una superficie de revolución porque se engendra con una recta que gira en torno a un eje pero no es de revolución de doble curvatura porque la que gira es una recta y no una línea curva.
La esfera sí que es una superficie de revolución de doble curvatura ya que es una curva que gira en torno a uno de sus diámetros.
Todas las curvas cónicas generan al girar la cónica sobre un eje una superficie de revolución de doble curvatura, la elipse genera el elipsoide, la hipérbola el hiperboloide, la circunferencia la esfera o el toro, la parábola el paraboloide, etcétera.
Si cogemos formas irregulares se tienen superficies complejas de revolución como pueden ser jarros, pies de lámparas etc. las superficies de doble curvatura no son desarrollables, pero se pueden aproximar mediante el desarrollo de superficies cilíndricas entre generatrices.
Todas las secciones ortogonales al eje de revolución son siempre círculos llamados paralelos, mientras que las secciones que pasan por el eje de revolución son meridianos.
Superficies de evolución:
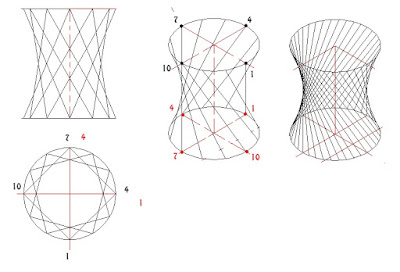
 Como refiere su nombre, son superficies que evolucionan con curvas o líneas de distinta forma. Superficie de evolución es aquella que evoluciona o se transforma, generándose por la unión de curvas distintas. En la figura un cuadrado se transforma de forma uniforme en una circunferencia. Para su construcción digital se utiliza el comando solevación. Su apariencia a veces es de una forma imposible, de una figura con una perspectiva mal dibujada -como la que aparenta el dibujo.
Como refiere su nombre, son superficies que evolucionan con curvas o líneas de distinta forma. Superficie de evolución es aquella que evoluciona o se transforma, generándose por la unión de curvas distintas. En la figura un cuadrado se transforma de forma uniforme en una circunferencia. Para su construcción digital se utiliza el comando solevación. Su apariencia a veces es de una forma imposible, de una figura con una perspectiva mal dibujada -como la que aparenta el dibujo.Como ejemplo de superficies de evolución o de desarrollo tenemos carrocerías de automóviles, fuselajes de aviones, casco de navíos y superficies irregulares complejas que suelen ser redondeadas y suaves y cuya definición del contorno no es suficiente para definirlas. La forma de definirlas es mediante proyecciones principales o secciones principales entre planos paralelos. Es algo análogo a lo que se hace en el sistema acotado, representar una montaña por líneas de contorno o de nivel, este es un ejemplo también del método que se viene haciendo desde hace años para la construcción de barcos.
Diseño de barcos: estas superficies contorneadas se generan mediante secciones ortogonales a los planos de proyección del conjunto de planos horizontales y verticales, que determinan puntos de la superficie y se proyectan generando, por ejemplo, en un casco de un barco, la línea de flotación en el alzado y en la planta y las cuadernas o secciones de planos verticales en el perfil.
Cada cuaderna que se muestra en la proyección vertical es la intersección de la superficie del barco con un plano vertical y otro horizontal. Las líneas de flotación que se indican en una proyección en planta representan las curvas de intersección con planos horizontales.
Se debe hacer un estudio muy profundo del carenado para que la superficie final sea suave. Para conseguirlo las curvas han de tener un radio de curvatura muy grande y se deben utilizar cónicas, que gozan de tener la propiedad de ser suaves, esto quiere decir, que no se nota la transición de una a otra. Las superficies generadas con cónicas son fuseladas y aerodinámicas.
Se demuestra en geometría proyectiva que para determinar una cónica son necesarios cinco elementos entre puntos y/o tangentes. Las tangentes nos sirven para definir la pendiente en cada punto de la cónica. De esta forma los puntos de los contornos de las superficies se pueden unir cada cinco elementos mediante una cónica y enlazarlo a continuación con otra cónica.
La hélice es una línea de doble curvatura que está generada por un punto que se desplaza de manera uniforme en torno a un eje, al tiempo que se desplaza siempre paralelo al mismo.
Es el resultado de componer un giro y una traslación; si el punto equidista siempre del eje, la hélice será cilíndrica mientras que si la distancia del punto al eje varía de manera uniforme según se mueve la hélice, será cónica. También se puede considerar la hélice como una circunferencia que gira mientras se desplaza en la dirección del eje. Cuando la circunferencia da una vuelta entera se le llama paso de la hélice. Puede rotar hacia la derecha o hacia la izquierda.
La principal aplicación de esta curva es el tornillo, además se utiliza en muelles cilíndricos y cónicos, taladros, brocas, fresas en espiral, escaleras de caracol, etcétera.
La hélice es el movimiento que describe un punto de una hélice de un avión cuando se mueve, también es la línea directriz de las superficies helicoidales.
Para construirla nos valemos de tres datos, el diámetro, el paso y la dirección de giro de la hélice. Para dibujarla basta con hacer circunferencias a diferentes alturas en un alzado y generatrices de un cilindro en planta proyectadas sobre el alzado. La intersección de la primera línea con la primera circunferencia es un punto de la curva, la de la segunda línea con la segunda circunferencia otro punto de la curva, y así sucesivamente. Cuantas más circunferencias y líneas tenga la figura más precisa saldrá dibujada la curva.
Como las circunferencias son equidistantes y las divisiones angulares son iguales para las generatrices, tenemos que el ángulo de inclinación de la hélice es siempre constante. El desarrollo de la figura es un triángulo, la base del triángulo es la rectificación de la circunferencia base del cilindro, la altura es la longitud del paso y la hipotenusa del triángulo es la verdadera magnitud de un giro completo de la hélice. El ángulo entre la hipotenusa y la base tiene siempre una pendiente constante.
La pendiente es la tangente del ángulo y para determinar su inclinación dividimos el paso entre la longitud de la circunferencia, o lo que es lo mismo, la altura del triángulo dividida entre la longitud de la circunferencia. Si queremos dibujar la tangente a la curva, debemos saber que tiene la misma pendiente que la hélice por lo que coincide con el desarrollo de la misma.
 Helicoide o hélice adaptado a un toro o "donuts" llamado helicoide tórico.
Helicoide o hélice adaptado a un toro o "donuts" llamado helicoide tórico.La hélice se puede adecuar a cualquier superficie adoptando el nombre propio más el de la superficie en la que se acomoda.
La superficie helizoidal se engendra por una línea recta que gira en torno a un eje al tiempo que se desplaza en la dirección del mismo. Si tomamos un helicoide y en uno de sus puntos colocamos una recta con una posición cualquiera, el desplazamiento de la recta por el helicoide genera un helizoide.
 El helicoide es la curva que engendra un punto al componer un movimiento de giro más otro de traslación, es el movimiento que describe un punto de una hélice de un avión cuando se mueve. Si ese punto que describe la hélice o helicoide lo unimos a su eje de revolución con líneas rectas tenemos una superficie helicoidal llamada helizoide, si estas líneas rectas son perpendiculares al eje tenemos un helicoide recto. El helicoide es un ejemplo particular de los pasamanos o del borde de los peldaños de una escalera de caracol.
El helicoide es la curva que engendra un punto al componer un movimiento de giro más otro de traslación, es el movimiento que describe un punto de una hélice de un avión cuando se mueve. Si ese punto que describe la hélice o helicoide lo unimos a su eje de revolución con líneas rectas tenemos una superficie helicoidal llamada helizoide, si estas líneas rectas son perpendiculares al eje tenemos un helicoide recto. El helicoide es un ejemplo particular de los pasamanos o del borde de los peldaños de una escalera de caracol.http://helicoides.blogspot.com/
Hélices esféricas
 Las líneas que pasan por el helicoide pueden ser oblicuas respecto al eje, con lo cual tenemos un helicoide oblicuo. Pueden cortar al eje o pueden cruzarse con él pudiendo producir superficies regladas alabeadas.
Las líneas que pasan por el helicoide pueden ser oblicuas respecto al eje, con lo cual tenemos un helicoide oblicuo. Pueden cortar al eje o pueden cruzarse con él pudiendo producir superficies regladas alabeadas. Los helicoides se pueden adecuar a cualquier tipo de superficie, en el primer caso (borde superior izquierdo) se adecuaron a una elipse de revolución que genera un elipsoide, con lo que tenemos un helicoide elipsoidal. En el segundo caso está adecuado a un toro sin agujero (un donette en color rojo), en el tercer caso en azul tendremos que está adecuado a un cono de revolución. Si en una espiral (http://curvas-planas.blogspot.com/) se estira ortogonal y uniformemente uno de sus vértices hasta alejarlo del plano en el que se aloja, obtenemos un helicoide cónico.
Los helicoides se pueden adecuar a cualquier tipo de superficie, en el primer caso (borde superior izquierdo) se adecuaron a una elipse de revolución que genera un elipsoide, con lo que tenemos un helicoide elipsoidal. En el segundo caso está adecuado a un toro sin agujero (un donette en color rojo), en el tercer caso en azul tendremos que está adecuado a un cono de revolución. Si en una espiral (http://curvas-planas.blogspot.com/) se estira ortogonal y uniformemente uno de sus vértices hasta alejarlo del plano en el que se aloja, obtenemos un helicoide cónico.En magenta tenemos un muelle contraído por uno de los bordes, en el azul lo tenemos con una torsión, etcétera.
 Cuando en vez de desplazarse un punto para generar el helicoide, lo que se desplaza es una esfera, tenemos un objeto llamado serpentín.
Cuando en vez de desplazarse un punto para generar el helicoide, lo que se desplaza es una esfera, tenemos un objeto llamado serpentín. Como el serpentín es un muelle en cuyas secciones transversales al movimiento de la esfera que engendra la superficie son circunferencias tenemos que también se engendra al desplazar una circunferencia a lo largo de la trayectoria del helicoide siendo los puntos del helicoide centros de la circunferencia y ésta ortogonal al eje de desplazamiento.
Como el serpentín es un muelle en cuyas secciones transversales al movimiento de la esfera que engendra la superficie son circunferencias tenemos que también se engendra al desplazar una circunferencia a lo largo de la trayectoria del helicoide siendo los puntos del helicoide centros de la circunferencia y ésta ortogonal al eje de desplazamiento.Una convoluta helicoidal es la superficie generada por una línea recta que es tangente a la hélice. Para definirla necesitamos la directriz helicoidal dada y un punto de tangencia.
Esta superficie se puede colocar entre dos superficies cilíndricas concéntricas para determinar en la planta los dos puntos de intersección de cada recta con los cilindros y obtener el contorno de los dos helicoides que son las directrices de la superficie.
El helizoide recto es una superficie reglada alabeada cuya generatriz se mueve siempre en contacto con dos hélices concéntricas. Estas hélices son sus directrices y forman un ángulo siempre igual con sus ejes. Si la generatriz es ortogonal tenemos un helicoide recto, si no lo es tenemos uno oblicuo. El helicoide recto que tiene una generatriz incidente en el eje entra dentro de la clasificación del conoide, ya que todos sus elementos son paralelos al plano director.
El helizoide oblicuo es aquel cuya generatriz se traslada siempre mediante un mismo ángulo.
La superficie helicoidal posee muchas aplicaciones, la rosca cuadrada helicoidal posee una superficie lateral que es un helicoide recto, los muelles de arrollamientos helicoidales. Las roscas de tornillos, los muelles de las bobinas, los resortes, las roscas de los taladros, las escaleras de caracol, etcétera.
Superficies radiadas: conos, cilindros, prismas y pirámides.
 El cilindro es una una superficie de revolución y reglada. Las superficies radiadas son regladas (eso quiere decir que si tomamos una generatriz de la misma podemos seguir toda su superficie con el canto de una regla) y desarrollables (se pueden extender sobre un plano) además pueden ser cilíndricas o prismáticas si el punto de contacto con la regla está en el infinito.
El cilindro es una una superficie de revolución y reglada. Las superficies radiadas son regladas (eso quiere decir que si tomamos una generatriz de la misma podemos seguir toda su superficie con el canto de una regla) y desarrollables (se pueden extender sobre un plano) además pueden ser cilíndricas o prismáticas si el punto de contacto con la regla está en el infinito.El cilindro es también una superficie radiada que quiere decir que si tomamos una generatriz de la misma podemos seguir toda su superficie con el canto de una regla y un punto del canto de esta regla pasa siempre por un punto fijo de la superficie, esto es, que la regla toca un punto sobre la superficie de forma invariable -e ideal si está en el infinito, como el caso del cilindro o prisma.
 Un prisma oblicuo a la izquierda y otro recto a la derecha. El desplazamiento o extrusión de un polígono en una trayectoria recta u oblicua genera un prisma recto u oblicuo, respectivamente. El prisma es otra superficie radiada de tipo cilíndrica porque las líneas que unen sus bases están unidas por líneas paralelas. La superficie radiada cilíndrica es un caso particular de la cónica en la que el vértice por donde pasan los radios está en el infinito. Superficie prismática es la que se genera por una recta que se mueve siempre paralela a otra y en una trayectoria poligonal quebrada que está sobre un plano distinto a ella.
Un prisma oblicuo a la izquierda y otro recto a la derecha. El desplazamiento o extrusión de un polígono en una trayectoria recta u oblicua genera un prisma recto u oblicuo, respectivamente. El prisma es otra superficie radiada de tipo cilíndrica porque las líneas que unen sus bases están unidas por líneas paralelas. La superficie radiada cilíndrica es un caso particular de la cónica en la que el vértice por donde pasan los radios está en el infinito. Superficie prismática es la que se genera por una recta que se mueve siempre paralela a otra y en una trayectoria poligonal quebrada que está sobre un plano distinto a ella. El cono es una superficie radiada de tipo cónica que se engendra por una recta que gira en torno a un eje, ambas en el mismo plano. La línea o curva directriz es la que corta a todas las generatrices y es en este caso una circunferencia. La curva directriz es una sección del cono.
El cono es una superficie radiada de tipo cónica que se engendra por una recta que gira en torno a un eje, ambas en el mismo plano. La línea o curva directriz es la que corta a todas las generatrices y es en este caso una circunferencia. La curva directriz es una sección del cono. La pirámide es otro tipo de superficie radiada de tipo cónico porque tiene su vértice localizado en un punto propio. La directriz es un polígono regular o irregular y la pirámide es recta si su vértice incide en la recta perpendicular a la base, si no es, como en este caso, una pirámide oblicua. Es una superficie reglada, ya que una regla que pase por su vértice puede seguir todas las caras de la superficie, y es además desarrollable, que quiere decir que sus caras se pueden extender sobre un plano y poder construirla de papel.
La pirámide es otro tipo de superficie radiada de tipo cónico porque tiene su vértice localizado en un punto propio. La directriz es un polígono regular o irregular y la pirámide es recta si su vértice incide en la recta perpendicular a la base, si no es, como en este caso, una pirámide oblicua. Es una superficie reglada, ya que una regla que pase por su vértice puede seguir todas las caras de la superficie, y es además desarrollable, que quiere decir que sus caras se pueden extender sobre un plano y poder construirla de papel. Una superficie de revolución es la que se genera al girar una recta o curva alrededor de otra recta llamada eje de giro, siendo ambas coplanarias.
Una superficie de revolución es la que se genera al girar una recta o curva alrededor de otra recta llamada eje de giro, siendo ambas coplanarias.Si cortamos la superficie por un plano ortogonal al eje tenemos una circunferencia llamada paralelo. Toda superficie de revolución tiene un paralelo de radio máximo y mínimo, denominados respectivamente círculos de ecuador y de garganta.
Todo plano que corta la figura y que incida en el eje de la superficie de revolución se llama meridiano. El meridiano de plano frontal es el que corresponde al contorno de la superficie en alzado. Los meridianos son líneas curvas simétricas respecto al eje de revolución, y la superficie es siempre simétrica respecto a cualquier plano meridiano que pase por el eje.
Cada punto de la superficie contiene a un paralelo y a un meridiano, excepto si la superficie corta al eje en un punto, en este caso por el punto pasan todos los meridianos.
Toda superficie de revolución queda definida por la curva o línea generatriz y su eje, estando ambas en un mismo plano.
Todo plano tangente a la superficie de revolución está definido por las líneas tan gentes a dos curvas de la superficie que pasen por él.
Como caso particular tenemos las tangentes que definen el meridiano y paralelo que pasan por un punto.
El plano tangente en un punto es perpendicular al plano meridiano que pasa por el punto. Todos los paralelos y meridianos se cortan entre sí perpendicularmente.
La superficie envolvente de los planos tangentes en todos los puntos de los paralelos y de los meridianos es un cono y un cilindro circunscrito a ella, respectivamente.
Todas las rectas perpendiculares a la superficie en todos los puntos de cualquier paralelo se dirigen siempre a un punto del eje.
 La esfera es una superficie de revolución, pues se engendra por una semicircunferencia que gira en torno a un eje de revolución que es su diámetro.
La esfera es una superficie de revolución, pues se engendra por una semicircunferencia que gira en torno a un eje de revolución que es su diámetro.Es una superficie de doble curvatura, esto quiere decir que es curva en dos direcciones distintas. Todos sus puntos son elípticos, o sea que en el entorno de un punto las curvas tienen el mismo sentido y es una superficie de segundo grado porque una recta la corta como máximo en dos puntos. La esfera es una superficie no desarrollable, por tanto no se puede extender sobre un plano.
En una esfera se puede representar lo que aparece en un plano conservando los ángulos mediante una proyección llamada estereográfica:
http://proyeccion-estereografica.blogspot.com/
De ahí que se utilice mucho en cartografía (construcción de mapas) http://construccion-de-mapas.blogspot.com/, y por ejemplo en la cartografía celeste:
http://cartografia-celeste.blogspot.com/
Tambien se conservan los ángulos en una transformación del espacio exterior en el interior de la esfera, esto es, en la inversión del espacio en la esfera:
http:// tangencias-inversion.blogspot.com/
Geometría no euclídea de la esfera:
http://geometria-de-la-esfera.blogspot.com/
 El toro (figura semejante a un donuts) es una superficie de revolución engendrada por una circunferencia que gira en torno a un eje que no pasa por su centro, ambas en el mismo plano. Las secciones de un toro son las llamadas curvas de Cassini, la sección por desplazamiento por un borde de la figura genera primero una curva parecida a una circunferencia cada vez más excéntrica hasta generar otra curva parecida a la elipse que se va alargando y sus extremos se van haciendo cada vez más rectos hasta estrecharse por el medio y llegarse a cortar produciendo una figura parecida al símbolo del infinito llamada lemniscata (sección AA), curva inversa de la hipérbola y utilizada como curva de transición progresiva para enlazar vías de autopista (como la clotoide para el trazado de curvas suaves).
El toro (figura semejante a un donuts) es una superficie de revolución engendrada por una circunferencia que gira en torno a un eje que no pasa por su centro, ambas en el mismo plano. Las secciones de un toro son las llamadas curvas de Cassini, la sección por desplazamiento por un borde de la figura genera primero una curva parecida a una circunferencia cada vez más excéntrica hasta generar otra curva parecida a la elipse que se va alargando y sus extremos se van haciendo cada vez más rectos hasta estrecharse por el medio y llegarse a cortar produciendo una figura parecida al símbolo del infinito llamada lemniscata (sección AA), curva inversa de la hipérbola y utilizada como curva de transición progresiva para enlazar vías de autopista (como la clotoide para el trazado de curvas suaves).A partir de esta sección el desplazamiento produce la separación de los dos trozos de la lemniscata en curvas parecidas a elipses hasta transformarse en circunferencias simétricas respecto al eje.
El toro es una superficie de cuarto orden, esto es el número máximo de puntos con que la puede atravesar una recta, que son cuatro.

 Una superficie de revolución está engendrada por una línea o curva que gira en torno a un eje y es coplanaria con él. En el dibujo vemos las distintas posiciones de una parábola que gira en torno a un eje que a veces es secante (los tres casos de la izquierda), otras es exterior (la figura de color roja) y otra es tangente (la figura violeta). El paraboloide es la figura verde, engendrada por el giro de media parábola en torno a su eje de revolución.
Una superficie de revolución está engendrada por una línea o curva que gira en torno a un eje y es coplanaria con él. En el dibujo vemos las distintas posiciones de una parábola que gira en torno a un eje que a veces es secante (los tres casos de la izquierda), otras es exterior (la figura de color roja) y otra es tangente (la figura violeta). El paraboloide es la figura verde, engendrada por el giro de media parábola en torno a su eje de revolución. Paraboloide elíptico engendrado por una parábola que gira en torno a su eje. Como toda superficie de revolución todas las secciones ortogonales a su eje son circunferencias mientras que todas las que pasan por el eje determinan la curva de revolución que engendra la superficie. Las secciones ortogonales se llaman paralelos y las que pasan por el eje se llaman meridianos.
Paraboloide elíptico engendrado por una parábola que gira en torno a su eje. Como toda superficie de revolución todas las secciones ortogonales a su eje son circunferencias mientras que todas las que pasan por el eje determinan la curva de revolución que engendra la superficie. Las secciones ortogonales se llaman paralelos y las que pasan por el eje se llaman meridianos.
Superficies de 2º grado, o cuádricas o cuadráticas son aquellas superficies algebraicas que tienen una ecuación de segundo grado (elipsoide, paraboloide elíptico, hiperboloide de revolución o de dos hojas, etc.)
Una recta puede cortar a una cuádrica en un punto, dos o ninguno. Si tiene 3 sobre la cuádrica, la recta pertenece a la superficie. Una cuádrica tiene en cada punto un plano tangente, si tuviera más decimos que la superficie tiene puntos múltiples, cosa que no sucede en estas superficies.

Toda superficie cuadrática tiene dos tipos de puntos, elípticos o hiperbólicos.
Las cuádricas elípticas son superficies que no pueden ser generadas por rectas mientras que las hiperbólicas sí que pueden, de ahí que a las elípticas se les llame cuádricas no regladas y a las hiperbólicas se les llame cuádricas regladas.
En una cuádrica elíptica un plano puede ser secante de manera que la corta siempre según una cónica, si es tangente el plano toca a la cuádrica en un punto y si es exterior no la corta.
Cuando el plano del infinito es exterior a la cuádrica tenemos un elipsoide, si el plano es tangente a la cuádrica tenemos un paraboloide elíptico y si corta a la misma tenemos un hiperboloide de revolución o de dos hojas.
Las tres superficies cuadráticas se engendran por la revolución de la elipse, parábola o hipérbola tomando como eje de revolución su eje de simetría
Toda cuádrica hipérbólica contiene dos grupos de generatrices de distinto sistema, a cada uno se le llama haz alabeado.
La cuádrica reglada no contiene planos exteriores, cualquier plano del espacio la corta en infinitos puntos de sus generatrices generando una cónica, cuyo caso particular puede degenerar en dos rectas. Todo plano secante la corta según una cónica, mientras que si es tangente corta a la superficie en dos rectas, de las que su punto de intersección es el punto de contacto del plano tangente a la superficie.
Cuando el plano que está en infinito es tangente a la cuádrica tenemos el paraboloide hiperbólico, mientras que si el plano es secante tenemos un hiperboloide de una hoja o hiperboloide reglado.
Propiedades: por cada punto de la superficie cuadrática pasa una generatriz de cada uno de los dos sistemas. Dos generatrices de un mismo sistema e infinitamente próximas se cruzan mientras que las de distinto sistema se cortan. Las generatrices de los distintos sistemas se cortan en series proyectivas de puntos.
Podemos dibujar estas figuras mediante las generatrices de un sistema que quedan determinadas por tres puntos colineales de tres generatrices distintas del otro sistema. Si tomamos dos generatrices de distinto sistema que se corten, por el punto de intersección pasa un plano tangente a la cuádrica.

Superficie poliédrica es la que está constituida por varios planos que se cortan entre sí.
Poliedros regulares son los que tienen todas las caras iguales, y son polígonos regulares,-figuras planas que tienen todos los lados y ángulos iguales. Existen sólo cinco y tienen numerosas propiedades: se pueden inscribir unos dentro de otros de diversas formas, se pueden inscribir y circunscribir en una esfera, se pueden prolongar sus aristas obteniéndose otro de ellos, etc. En la figura se observa un icosaedro regular, que es una figura de 20 caras que son polígonos regulares, con sus dos proyecciones planas idénticas en planta y alzado tras un giro de 90° y desplazamiento de una de las vistas.
Pincha en el enlace para bajar un manual sobre los poliedros regulares:
http://www.box.net/shared/lpxg66qqvg
Ejemplos de transformación de superficies poliédricas:
http://inscripcionpoliedrica.blogspot.com/
http://dodecaedro-regular.blogspot.com/
http://icosaedro-regular.blogspot.com/
http://transformacion-de-poliedros.blogspot.com/
http://icosaedroendodecaedro.blogspot.com/
http://superficiespoliedricas.blogspot.com/
http://transformaciondesuperficies.blogspot.com/
http://lospoliedrosregulares.blogspot.com/
http://superficiestransformadas.blogspot.com/
http://metamorfosisgeometrica.blogspot.com/
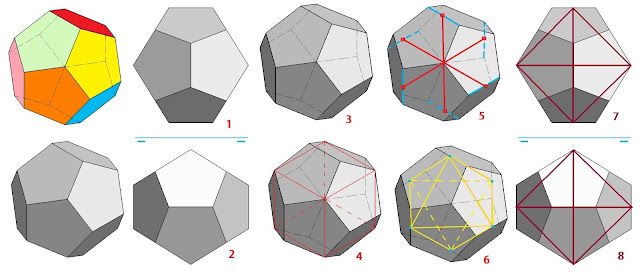
poliedro de 12 caras pentagonales regulares, en el número 3 observamos esa figura
en axonometría isométrica, en el número 40 vemos la misma figura que contiene a
un cubo inscrito y que pasa por algunos de sus vértices, en la figura número 5 podemos
observar que los tres ejes ortogonales- en color rojo- tienen el mismo tamaño,
eso quiere decir que podemos inscribir también en el dodecaedro regular un octaedro regular
- en color amarillo- tal y como aparece en la figura 6.
dodecaedro regular, observamos además en la figura las proyecciones en
planta y alzado del octaedro regular inscrito en la figura.
Sección oblicua de cono en diédrico y desarrollo
Desarrollo de esfera y ejemplo práctico
 Desarrollar una superficie es extenderla sobre un plano, es coger sus caras y anexionarlas en un plano poniéndolas unidas por sus lados hasta convertirla en una figura plana, de manera que si se recortan los bordes y se doblan por los lados se puede construir en tres dimensiones.
Desarrollar una superficie es extenderla sobre un plano, es coger sus caras y anexionarlas en un plano poniéndolas unidas por sus lados hasta convertirla en una figura plana, de manera que si se recortan los bordes y se doblan por los lados se puede construir en tres dimensiones. Aquí observamos el desarrollo de otra superficie, el cuboctaedro rombitruncado. Esta superficie es un poliedro arquimediano, obtenido por la sección de las caras de un poliedro regular.
Aquí observamos el desarrollo de otra superficie, el cuboctaedro rombitruncado. Esta superficie es un poliedro arquimediano, obtenido por la sección de las caras de un poliedro regular. Diagrama de Schlegel. Si observamos una figura de cristal muy cerca de manera que todas sus aristas queden detrás de una cara, estaremos viendo la figura representada en este diagrama. Para construir figuras según este procedimiento se tiene que dar el caso de que las aristas no se corten entre sí y al mismo tiempo aparezcan todos los vértices y aristas de la figura en su representación. Este diagrama facilita que en las superficies poliédricas, el control de los vértices, de las líneas que pasan por cada vértice, de los lados, etcétera.
Diagrama de Schlegel. Si observamos una figura de cristal muy cerca de manera que todas sus aristas queden detrás de una cara, estaremos viendo la figura representada en este diagrama. Para construir figuras según este procedimiento se tiene que dar el caso de que las aristas no se corten entre sí y al mismo tiempo aparezcan todos los vértices y aristas de la figura en su representación. Este diagrama facilita que en las superficies poliédricas, el control de los vértices, de las líneas que pasan por cada vértice, de los lados, etcétera. Prisma de base hexagonal regular recto. Un prisma es una superficie poliédrica reglada desarrollable. Si las aristas laterales que unen las bases son oblicuas respecto a ellas estaremos hablando de un prisma oblicuo, si no lo son, hablaremos de un prisma recto.
Prisma de base hexagonal regular recto. Un prisma es una superficie poliédrica reglada desarrollable. Si las aristas laterales que unen las bases son oblicuas respecto a ellas estaremos hablando de un prisma oblicuo, si no lo son, hablaremos de un prisma recto. Poliedros duales como el icosaedro y el dodecaedro tienen una propiedad curiosa: si prolongamos las aristas del icosaedro regular se cortan en vértices que determinan los puntos de un dodecaedro. Recíprocamente si prolongamos las aristas del dodecaedro regular se cortan en vértices que determinar los puntos de un icosaedro. Ambas figuras, junto con el cubo en el que se pueden inscribir, tienen sus aristas relacionadas en una proporción áurea. La arista del dodecaedro más la arista del icosaedro es igual a la arista del cubo en el que están inscritos. La relación anterior además de la siguiente pone en relación a los tres elementos en la proporción áurea: la arista del cubo es a la arista del icosaedro como la del icosaedro es a la del dodecaedro, en geometría se dice que la arista del icosaedro es media proporcional entre la arista del cubo y la arista del dodecaedro.
Poliedros duales como el icosaedro y el dodecaedro tienen una propiedad curiosa: si prolongamos las aristas del icosaedro regular se cortan en vértices que determinan los puntos de un dodecaedro. Recíprocamente si prolongamos las aristas del dodecaedro regular se cortan en vértices que determinar los puntos de un icosaedro. Ambas figuras, junto con el cubo en el que se pueden inscribir, tienen sus aristas relacionadas en una proporción áurea. La arista del dodecaedro más la arista del icosaedro es igual a la arista del cubo en el que están inscritos. La relación anterior además de la siguiente pone en relación a los tres elementos en la proporción áurea: la arista del cubo es a la arista del icosaedro como la del icosaedro es a la del dodecaedro, en geometría se dice que la arista del icosaedro es media proporcional entre la arista del cubo y la arista del dodecaedro. Aquí observamos una proyección axonométrica del icosaedro al que se han prolongado sus aristas y en su intersección se generan los vértices de un dodecaedro regular. Al añadir las pirámides hemos obtenido el gran dodecaedro estrellado.
Aquí observamos una proyección axonométrica del icosaedro al que se han prolongado sus aristas y en su intersección se generan los vértices de un dodecaedro regular. Al añadir las pirámides hemos obtenido el gran dodecaedro estrellado.Se puede obtener por tanto un poliedro estrellado al incorporar pirámides en cada una de las caras de un poliedro regular, de esta forma sobre el icosaedro con las pirámides sobre sus caras también los vértices se inscriben en un dodecaedro regular.
 Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.
Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.Esfera geodésica hexaédrica de frecuencia 2
http://youtu.be/L9txE6QS_oM
Esfera geodésica octaédrica de frecuencia 2
http://youtu.be/j1-IH6nDJ9E
Esfera geodésica octaédrica de frecuencia 3
http://youtu.be/AtBK88YRGmY
Esfera geodésica octaédrica de frecuencia 3 con proyecciones diédricas iguales
http://youtu.be/6RC4JfP9Eqc
Esfera geodésica octaédrica de frecuencia 4.
http://youtu.be/D1ZZkYXNBys
Esfera geodésica dodecaédrica de frecuencia 1
http://youtu.be/PbGG8EF6IMc
Esfera geodésica dodecaédrica de frecuencia 2
http://youtu.be/hG35S3RSL3M
Esfera geodésica icosaédrica de frecuencia 2
http://youtu.be/8AtDgFxdHwk
Esfera geodésica icosaédrica de frecuencia 3
http://youtu.be/qQNwmCCm488
Esfera geodésica icosaédrica de frecuencia 4
http://youtu.be/EWmKh2wpIdc
 Los poliedros arquimedianos son superficies regladas desarrollables producidas en la mayor parte de los casos por secciones de los poliedros regulares (en el dibujo, todos se pueden obtener por secciones de los poliedros regulares menos los duplicados en sentidos distintos: el cubo romo y dodecaedro romo). Tienen bastante regularidad y todas las caras de los poliedros arquimedianos son polígonos regulares.
Los poliedros arquimedianos son superficies regladas desarrollables producidas en la mayor parte de los casos por secciones de los poliedros regulares (en el dibujo, todos se pueden obtener por secciones de los poliedros regulares menos los duplicados en sentidos distintos: el cubo romo y dodecaedro romo). Tienen bastante regularidad y todas las caras de los poliedros arquimedianos son polígonos regulares.
Otra colocación en diédrico del rombicosidodecaedro y su representación axonométrica isométrica.
 En la figura de la izquierda observamos un icosidodecaedro - con la línea de tierra de color rojo-, esa figura se obtiene del icosaedro -Con la línea de tierra en color azul- o del dodecaedro cortándolo por un corte de tipo 1, o sea, cogiendo los puntos medios de cada arista y uniendolos, de esta forma obtenemos nuevas aristas y nos sale esta figura que aparece en el centro en color verde, en la parte superior.
En la figura de la izquierda observamos un icosidodecaedro - con la línea de tierra de color rojo-, esa figura se obtiene del icosaedro -Con la línea de tierra en color azul- o del dodecaedro cortándolo por un corte de tipo 1, o sea, cogiendo los puntos medios de cada arista y uniendolos, de esta forma obtenemos nuevas aristas y nos sale esta figura que aparece en el centro en color verde, en la parte superior.-----------------------------
con la figura inscrita dentro del dodecaedro- figuras M y N.
En la siguiente página podemos observar la construcción del rombicosidodecaedro (p. arquimediano) a partir del truncamiento de un icosaedro:
http://transformaciondesuperficies.blogspot.com/
Página en la que se puede ver la construcción de varios poliedros arquimedianos a partir de otros más sencillos, como los regulares.
Transformación de un poliedro regular (icosaedro) en distintos poliedros arquimedianos y regreso a otro poliedro regular: el dodecaedro.
http://arquimedianosendiedrico.blogspot.com/
http://poliedrosregularesyarquimedianos.blogspot.com/
 Aquí tenemos el ejemplo de un poliedro arquimediano generado por el truncamiento del icosaedro regular.
Aquí tenemos el ejemplo de un poliedro arquimediano generado por el truncamiento del icosaedro regular.Es la figura que se utiliza en los balones de fútbol clásicos, se pensaba hasta no hace mucho que sin gran número de aristas tenía una gran esfericidad (86,74% de redondez), hoy en día se utilizan otros con una estructura más esférica como el rombicosidodecaedro con un 94%.
 Los poliedros de Catalan son superficies duales de los arquimedianos. Los centros de las caras de los de Catalan son vértices de poliedros arquimedianos.
Los poliedros de Catalan son superficies duales de los arquimedianos. Los centros de las caras de los de Catalan son vértices de poliedros arquimedianos. El poliedro anterior en sistema axonométrico.
El poliedro anterior en sistema axonométrico. Los poliedros estrellados se pueden construir de forma general sumando pirámides a las caras de poliedros. Los más estudiados son el pequeño dodecaedro estrellado, el gran dodecaedro, el gran dodecaedro estrellado, y el gran icosaedro. Se pueden transformar unos en otros: el gran dodecaedro en pequeño dodecaedro estrellado y recíprocamente y el gran dodecaedro estrellado en el gran icosaedro y recíprocamente. Fueron estudiados por Kepler, Poinsont, Cauchy, etc.
Los poliedros estrellados se pueden construir de forma general sumando pirámides a las caras de poliedros. Los más estudiados son el pequeño dodecaedro estrellado, el gran dodecaedro, el gran dodecaedro estrellado, y el gran icosaedro. Se pueden transformar unos en otros: el gran dodecaedro en pequeño dodecaedro estrellado y recíprocamente y el gran dodecaedro estrellado en el gran icosaedro y recíprocamente. Fueron estudiados por Kepler, Poinsont, Cauchy, etc. En la figura observamos en sistema diédrico y en vista axonométrica un icosaedro regular al que se le han añadido pirámides sobre sus caras, obteniendo de esta forma un poliedro estrellado.
En la figura observamos en sistema diédrico y en vista axonométrica un icosaedro regular al que se le han añadido pirámides sobre sus caras, obteniendo de esta forma un poliedro estrellado. Poliedros compuestos son los que están formados por varios poliedros que tienen el mismo centro. En la imagen vemos dos icosaedros regulares obtenidos por un giro de uno respecto al otro sobre uno de los ejes que pasa por los vértices.
Poliedros compuestos son los que están formados por varios poliedros que tienen el mismo centro. En la imagen vemos dos icosaedros regulares obtenidos por un giro de uno respecto al otro sobre uno de los ejes que pasa por los vértices.http://poliedroscompuestos.blogspot.com/
 Poliedros de Johnson son aquellos que siendo convexos y sin ser regulares ni arquimedianos, están formados por caras que son polígonos regulares.
Poliedros de Johnson son aquellos que siendo convexos y sin ser regulares ni arquimedianos, están formados por caras que son polígonos regulares. Johnson construyó todos los polígonos que entraban dentro de esta clasificación. En la imagen aparecen unos cuantos.
Johnson construyó todos los polígonos que entraban dentro de esta clasificación. En la imagen aparecen unos cuantos. El dodecaedro truncado y Triaquisicosaedro son dos poliedros duales, el arquimediano se puede inscribir en el de Catalan de forma que en este último tomamos los puntos medios de las caras y los unimos.
El dodecaedro truncado y Triaquisicosaedro son dos poliedros duales, el arquimediano se puede inscribir en el de Catalan de forma que en este último tomamos los puntos medios de las caras y los unimos.http://icosaedrotriakis.blogspot.com/
 Observamos que la recíproca no es cierta y el triaquisicosaedro no se puede inscribir en el dodecaedro truncado de forma que los vértices del poliedro de Catalan estén sobre los puntos medios de las caras del arquimediano.
Observamos que la recíproca no es cierta y el triaquisicosaedro no se puede inscribir en el dodecaedro truncado de forma que los vértices del poliedro de Catalan estén sobre los puntos medios de las caras del arquimediano. Aquí vemos otra vista en la que el arquimediano está inscrito en el de Catalan. El triaquisicosaedro no es otra cosa que el icosaedro con pirámides sobre sus caras, de ahí su nombre con el prefijo triakis-, denominación que designa en los poliedros de Catalan este detalle.
Aquí vemos otra vista en la que el arquimediano está inscrito en el de Catalan. El triaquisicosaedro no es otra cosa que el icosaedro con pirámides sobre sus caras, de ahí su nombre con el prefijo triakis-, denominación que designa en los poliedros de Catalan este detalle.Los poliedros de Catalan poseen una esfera inscrita y los arquimedianos circunscrita
 Si cogemos los puntos medios de las caras de un antiprisma y los unimos con sus vértices más cercanos, obtenemos la figura dual de un antiprisma que es el deltoedro. Es una figura utilizada en dados, ya que puede tener número de caras ilimitada y al ser homogénea y todas sus caras estar en igual disposición respecto al centro, hay las mismas posibilidades de que caiga cualquier cara en un lanzamiento del dado.
Si cogemos los puntos medios de las caras de un antiprisma y los unimos con sus vértices más cercanos, obtenemos la figura dual de un antiprisma que es el deltoedro. Es una figura utilizada en dados, ya que puede tener número de caras ilimitada y al ser homogénea y todas sus caras estar en igual disposición respecto al centro, hay las mismas posibilidades de que caiga cualquier cara en un lanzamiento del dado. Proyección axonométrica de un deltoedro, está formado por caras en forma de Delta, trapezoides con un eje de simetría.
Proyección axonométrica de un deltoedro, está formado por caras en forma de Delta, trapezoides con un eje de simetría. Aquí observamos una dipirámide, es un poliedro formado por dos pirámides unidas, dual del prisma obtenido en la unión de los vértices centrales de cada cara del prisma.
Aquí observamos una dipirámide, es un poliedro formado por dos pirámides unidas, dual del prisma obtenido en la unión de los vértices centrales de cada cara del prisma. Vértices sobre caras: Otra posible inscripción de poliedros regulares: un tetraedro regular inscrito en un octaedro regular, tomando de este último los puntos medios de algunas caras (de todas tendríamos en este caso el cubo, su dual). Como los dos poliedros no son duales no cogemos todos los puntos de cada cara sino sólo algunos.
Vértices sobre caras: Otra posible inscripción de poliedros regulares: un tetraedro regular inscrito en un octaedro regular, tomando de este último los puntos medios de algunas caras (de todas tendríamos en este caso el cubo, su dual). Como los dos poliedros no son duales no cogemos todos los puntos de cada cara sino sólo algunos.






















































No hay comentarios:
Publicar un comentario